Hur uppnår man impedansmatchning av vågledare? Från transmissionsledningsteorin i mikrostripantennteorin vet vi att lämpliga serie- eller parallella transmissionsledningar kan väljas för att uppnå impedansmatchning mellan transmissionsledningar eller mellan transmissionsledningar och laster för att uppnå maximal effektöverföring och minimal reflektionsförlust. Samma princip för impedansmatchning i mikrostripledningar gäller för impedansmatchning i vågledare. Reflektioner i vågledarsystem kan leda till impedansavvikelser. När impedansförsämring inträffar är lösningen densamma som för transmissionsledningar, det vill säga att ändra det erforderliga värdet. Den klumpiga impedansen placeras vid förberäknade punkter i vågledaren för att övervinna avvikelsen och därigenom eliminera effekterna av reflektioner. Medan transmissionsledningar använder klumpiga impedanser eller stubbar, använder vågledare metallblock av olika former.
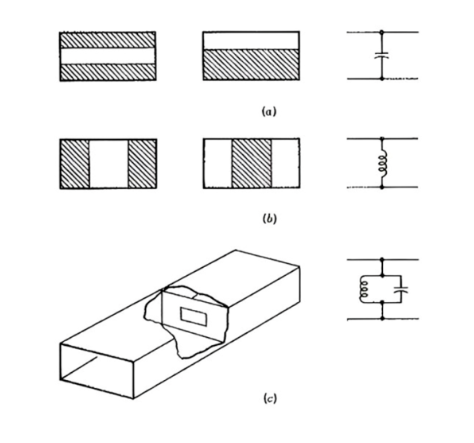

Figur 1: Vågledaririser och ekvivalent krets, (a) Kapacitiv; (b) Induktiv; (c) Resonant.
Figur 1 visar de olika typerna av impedansmatchning, i vilken som helst av de visade formerna och kan vara kapacitiv, induktiv eller resonant. Den matematiska analysen är komplex, men den fysiska förklaringen är det inte. Om man betraktar den första kapacitiva metallremsan i figuren kan man se att potentialen som fanns mellan vågledarens övre och nedre väggar (i dominantläge) nu finns mellan de två metallytorna i närmare varandra, så kapacitansen ökar. Däremot tillåter metallblocket i figur 1b ström att flyta där den inte flödade tidigare. Det kommer att finnas strömflöde i det tidigare förbättrade elektriska fältplanet på grund av tillägget av metallblocket. Därför sker energilagring i magnetfältet och induktansen vid den punkten av vågledaren ökar. Om formen och positionen på metallringen i figur c dessutom är rimligt utformade, kommer den induktiva reaktansen och den kapacitiva reaktansen som introduceras att vara lika, och aperturen kommer att vara parallellresonans. Detta innebär att impedansmatchningen och avstämningen av huvudläget är mycket god, och shunteffekten av detta läge kommer att vara försumbar. Andra lägen eller frekvenser kommer dock att dämpas, så den resonanta metallringen fungerar både som ett bandpassfilter och ett lägesfilter.
figur 2:(a) vågledarstolpar;(b) tvåskruvsmatchare
Ett annat sätt att finjustera visas ovan, där en cylindrisk metallstolpe sträcker sig från en av de breda sidorna in i vågledaren, vilket har samma effekt som en metallremsa när det gäller att ge klumpig reaktans vid den punkten. Metallstolpen kan vara kapacitiv eller induktiv, beroende på hur långt den sträcker sig in i vågledaren. I huvudsak går denna matchningsmetod ut på att när en sådan metallstolpe sträcker sig något in i vågledaren, ger den en kapacitiv susceptans vid den punkten, och den kapacitiva susceptansen ökar tills penetrationen är ungefär en fjärdedel av en våglängd. Vid denna punkt inträffar serieresonans. Ytterligare penetration av metallstolpen resulterar i en induktiv susceptans som minskar när insättningen blir mer fullständig. Resonansintensiteten vid mittpunktsinstallationen är omvänt proportionell mot kolonnens diameter och kan användas som ett filter, men i detta fall används den som ett bandstoppfilter för att överföra högre ordningsmoder. Jämfört med att öka impedansen hos metallremsor är en stor fördel med att använda metallstolpar att de är lätta att justera. Till exempel kan två skruvar användas som finjusteringsanordningar för att uppnå effektiv vågledarmatchning.
Resistiva belastningar och dämpare:
Precis som alla andra transmissionssystem kräver vågledare ibland perfekt impedansmatchning och avstämda belastningar för att helt absorbera inkommande vågor utan reflektion och för att vara frekvensokänsliga. En tillämpning för sådana terminaler är att göra olika effektmätningar på systemet utan att faktiskt utstråla någon effekt.
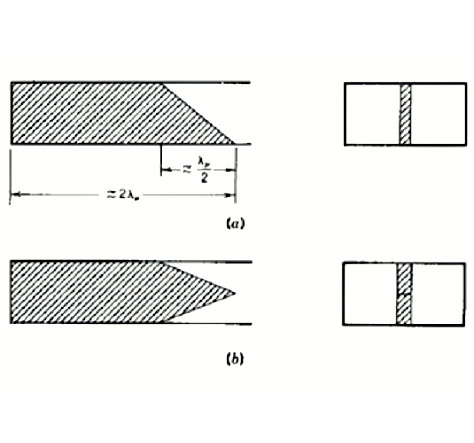
figur 3 vågledarmotståndsbelastning (a) enkel konisk (b) dubbel konisk
Den vanligaste resistiva avslutningen är en sektion av förlustbehäftat dielektrikum installerat i änden av vågledaren och avsmalnande (med spetsen pekande mot den inkommande vågen) för att inte orsaka reflektioner. Detta förlustbehäftade medium kan uppta hela vågledarens bredd, eller så kan det uppta endast mitten av vågledarens ände, som visas i figur 3. Avsmalningen kan vara enkel eller dubbel avsmalnande och har vanligtvis en längd på λp/2, med en total längd på ungefär två våglängder. Vanligtvis tillverkad av dielektriska plattor såsom glas, belagda med kolfilm eller vattenglas på utsidan. För högeffektsapplikationer kan sådana terminaler ha kylflänsar på utsidan av vågledaren, och effekten som levereras till terminalen kan avledas genom kylflänsen eller genom forcerad luftkylning.
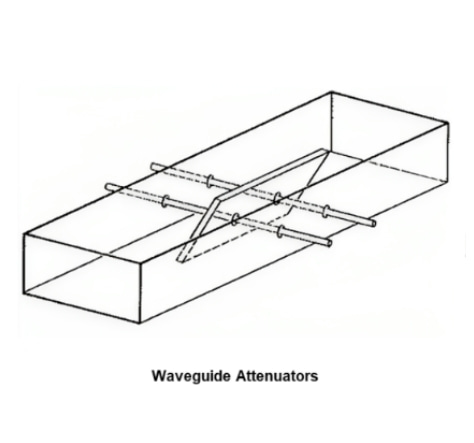
figur 4 Rörlig lamelldämpare
Dielektriska dämpare kan göras avtagbara som visas i figur 4. Placerade i mitten av vågledaren kan de flyttas i sidled från vågledarens centrum, där de ger störst dämpning, till kanterna, där dämpningen är kraftigt reducerad eftersom den elektriska fältstyrkan för den dominerande moden är mycket lägre.
Dämpning i vågledaren:
Energidämpningen hos vågledare omfattar huvudsakligen följande aspekter:
1. Reflektioner från interna vågledardiskontinuiteter eller feljusterade vågledarsektioner
2. Förluster orsakade av ström som flyter i vågledarväggar
3. Dielektriska förluster i fyllda vågledare
De två sista liknar motsvarande förluster i koaxialledningar och är båda relativt små. Denna förlust beror på väggmaterialet och dess ojämnhet, det använda dielektrikumet och frekvensen (på grund av skinneffekten). För mässingsrör är intervallet från 4 dB/100 m vid 5 GHz till 12 dB/100 m vid 10 GHz, men för aluminiumrör är intervallet lägre. För silverbelagda vågledare är förlusterna vanligtvis 8 dB/100 m vid 35 GHz, 30 dB/100 m vid 70 GHz och nära 500 dB/100 m vid 200 GHz. För att minska förluster, särskilt vid de högsta frekvenserna, är vågledare ibland pläterade (internt) med guld eller platina.
Som redan påpekats fungerar vågledaren som ett högpassfilter. Även om vågledaren i sig är praktiskt taget förlustfri, dämpas frekvenser under gränsfrekvensen kraftigt. Denna dämpning beror på reflektion vid vågledarmynningen snarare än utbredning.
Vågledarkoppling:
Vågledarkoppling sker vanligtvis genom flänsar när vågledardelar eller komponenter sammanfogas. Funktionen hos denna fläns är att säkerställa en smidig mekanisk anslutning och lämpliga elektriska egenskaper, särskilt låg extern strålning och låg intern reflektion.
Fläns:
Vågledarflänsar används ofta i mikrovågskommunikation, radarsystem, satellitkommunikation, antennsystem och laboratorieutrustning inom vetenskaplig forskning. De används för att ansluta olika vågledarsektioner, säkerställa att läckage och störningar förhindras och upprätthålla exakt inriktning av vågledaren för att säkerställa hög tillförlitlig överföring och exakt positionering av elektromagnetiska vågor med hög frekvens. En typisk vågledare har en fläns i varje ände, som visas i figur 5.
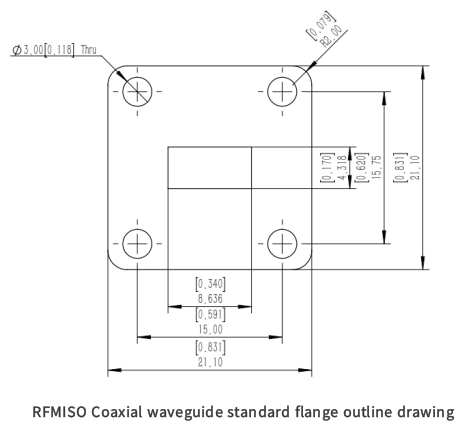
figur 5 (a) slät fläns; (b) flänskoppling.
Vid lägre frekvenser löds eller svetsas flänsen fast i vågledaren, medan man vid högre frekvenser använder en plattare, stumfläns. När två delar sammanfogas bultas flänsarna ihop, men ändarna måste vara slätbearbetade för att undvika diskontinuiteter i anslutningen. Det är uppenbarligen lättare att justera komponenterna korrekt med några justeringar, så mindre vågledare är ibland utrustade med gängade flänsar som kan skruvas ihop med en ringmutter. När frekvensen ökar minskar vågledarkopplingens storlek naturligtvis, och kopplingsdiskontinuiteten blir större i proportion till signalens våglängd och vågledarens storlek. Därför blir diskontinuiteter vid högre frekvenser mer besvärliga.
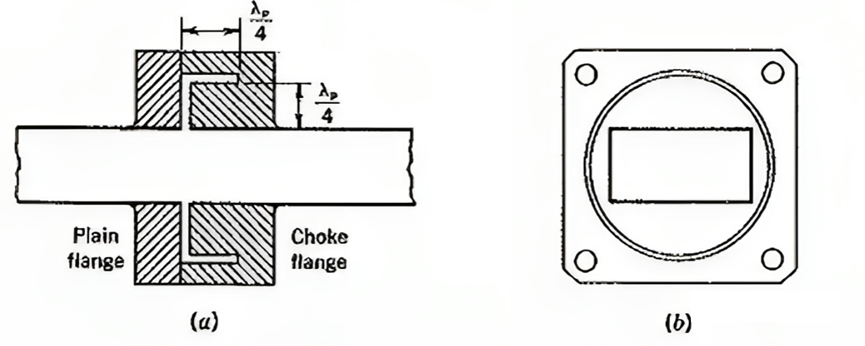
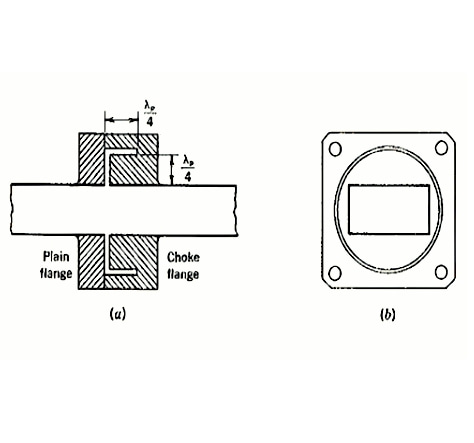
figur 6 (a) Tvärsnitt av chokekoppling; (b) Ändvy av chokefläns
För att lösa detta problem kan ett litet mellanrum lämnas mellan vågledarna, som visas i figur 6. En drosselkoppling bestående av en vanlig fläns och en drosselfläns sammankopplade. För att kompensera för eventuella diskontinuiteter används en cirkulär drosselring med L-format tvärsnitt i drosselflänsen för att uppnå en tätare anslutning. Till skillnad från vanliga flänsar är drosselflänsar frekvenskänsliga, men en optimerad design kan säkerställa en rimlig bandbredd (kanske 10 % av mittfrekvensen) över vilken stålwiren inte överstiger 1,05.
Publiceringstid: 15 januari 2024