Polarisering är en av antenners grundläggande egenskaper. Vi behöver först förstå polariseringen av planvågor. Sedan kan vi diskutera de viktigaste typerna av antennpolarisering.
linjär polarisering
Vi kommer att börja förstå polarisationen av en plan elektromagnetisk våg.
En plan elektromagnetisk (EM) våg har flera egenskaper. Den första är att energin färdas i en riktning (inget fält förändras i två ortogonala riktningar). För det andra är det elektriska fältet och magnetfältet vinkelräta mot varandra och ortogonala mot varandra. Elektriska och magnetiska fält är vinkelräta mot riktningen för planvågens utbredning. Som ett exempel, betrakta ett elektriskt fält med en frekvens (E-fält) som ges av ekvation (1). Det elektromagnetiska fältet färdas i +z-riktningen. Det elektriska fältet är riktat i +x-riktningen. Magnetfältet är i +y-riktningen.
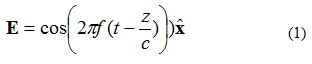
I ekvation (1), observera notationen: . Detta är en enhetsvektor (en längdvektor), vilket anger att den elektriska fältpunkten är i x-riktningen. Planvågen illustreras i figur 1.
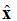
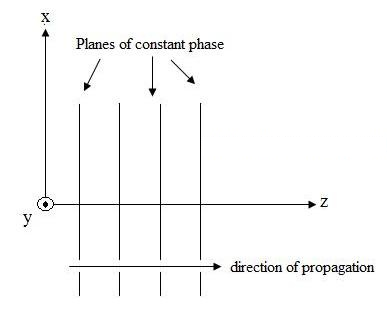
figur 1. Grafisk representation av det elektriska fältet som färdas i +z-riktningen.
Polarisering är spår- och utbredningsformen (konturen) för ett elektriskt fält. Som ett exempel kan vi betrakta ekvationen (1) för det planvågiga elektriska fältet. Vi kommer att observera positionen där det elektriska fältet är (X,Y,Z) = (0,0,0) som en funktion av tiden. Amplituden för detta fält är ritad i figur 2, vid flera tillfällen i tiden. Fältet oscillerar vid frekvensen "F".
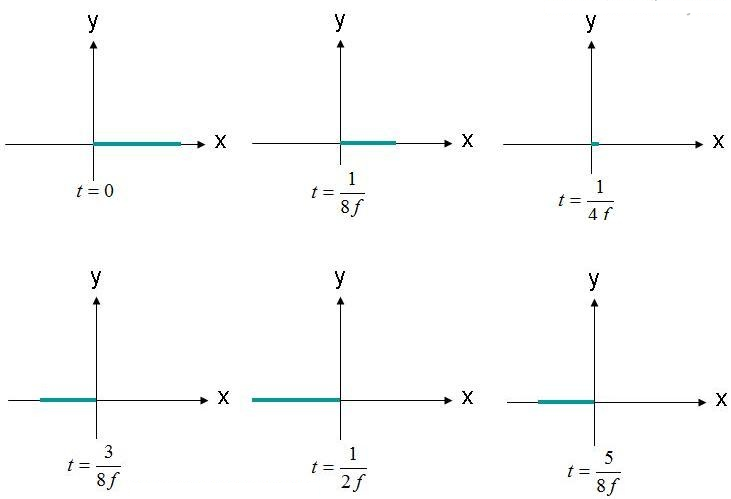
figur 2. Observera det elektriska fältet (X, Y, Z) = (0,0,0) vid olika tidpunkter.
Det elektriska fältet observeras vid origo och oscillerar fram och tillbaka i amplitud. Det elektriska fältet ligger alltid längs den angivna x-axeln. Eftersom det elektriska fältet upprätthålls längs en enda linje kan detta fält sägas vara linjärt polariserat. Dessutom, om x-axeln är parallell med marken, beskrivs detta fält också som horisontellt polariserat. Om fältet är orienterat längs y-axeln kan vågen sägas vara vertikalt polariserad.
Linjärt polariserade vågor behöver inte vara riktade längs en horisontell eller vertikal axel. Till exempel skulle en elektrisk fältvåg med en begränsning som ligger längs en linje som visas i figur 3 också vara linjärt polariserad.
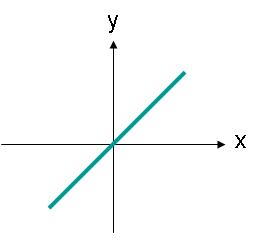
bild 3. Det elektriska fältets amplitud för en linjärt polariserad våg vars bana är en vinkel.
Det elektriska fältet i figur 3 kan beskrivas med ekvation (2). Nu finns det en x- och en y-komponent av det elektriska fältet. Båda komponenterna är lika stora.
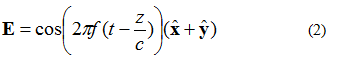
En sak att notera angående ekvation (2) är xy-komponenten och de elektroniska fälten i det andra steget. Detta innebär att båda komponenterna har samma amplitud hela tiden.
cirkulär polarisering
Antag nu att det elektriska fältet för en planvåg ges av ekvation (3):
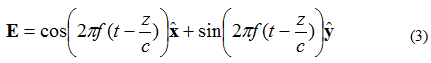
I detta fall är X- och Y-elementen 90 grader ur fas. Om fältet observeras som (X, Y, Z) = (0,0,0) igen som tidigare, kommer kurvan för det elektriska fältet kontra tiden att se ut som visas nedan i figur 4.
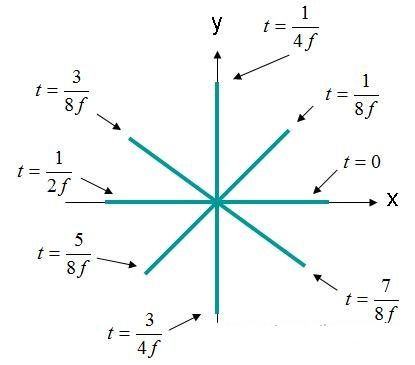
Figur 4. Elektrisk fältstyrka (X, Y, Z) = (0,0,0) EQ-domän. (3).
Det elektriska fältet i figur 4 roterar i en cirkel. Denna typ av fält beskrivs som en cirkulärt polariserad våg. För cirkulär polarisering måste följande kriterier vara uppfyllda:
- Standard för cirkulär polarisering
- Det elektriska fältet måste ha två ortogonala (vinkelräta) komponenter.
- De ortogonala komponenterna i det elektriska fältet måste ha lika amplituder.
- Kvadraturkomponenterna måste vara 90 grader ur fas.
Om fältet roterar på skärmen i vågfigur 4 sägs det vara moturs och högerhänt cirkulärpolariserat (RHCP). Om fältet roteras medurs kommer fältet att vara vänsterhänt cirkulärpolariserat (LHCP).
Elliptisk polarisering
Om det elektriska fältet har två vinkelräta komponenter, 90 grader ur fas men av samma magnitud, kommer fältet att vara elliptiskt polariserat. Om vi betraktar det elektriska fältet för en planvåg som rör sig i +z-riktningen, beskrivet av ekvation (4):
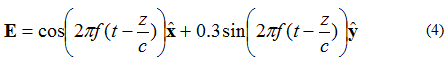
Orten för den punkt där spetsen på den elektriska fältvektorn kommer att anta ges i figur 5
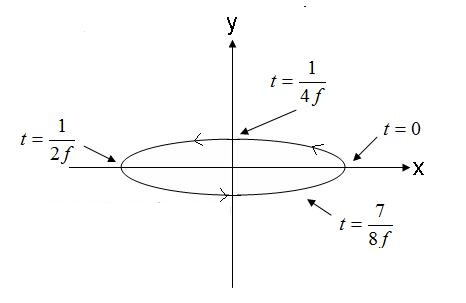
Figur 5. Prompt elliptiskt polarisationsvågs elektriskt fält. (4).
Fältet i figur 5, som rör sig moturs, skulle vara högerhänt elliptiskt om det rör sig utanför skärmen. Om den elektriska fältvektorn roterar i motsatt riktning kommer fältet att vara vänsterhänt elliptiskt polariserat.
Vidare hänvisar elliptisk polarisation till dess excentricitet. Förhållandet mellan excentricitet och amplituden hos huvud- och biaxeln. Till exempel är vågens excentricitet från ekvation (4) 1/0,3 = 3,33. Elliptiskt polariserade vågor beskrivs vidare av huvudaxelns riktning. Vågekvationen (4) har en axel som huvudsakligen består av x-axeln. Observera att huvudaxeln kan vara i vilken planvinkel som helst. Vinkeln krävs inte för att passa X-, Y- eller Z-axeln. Slutligen är det viktigt att notera att både cirkulär och linjär polarisation är specialfall av elliptisk polarisation. 1.0 excentrisk elliptiskt polariserad våg är en cirkulärt polariserad våg. Elliptiskt polariserade vågor med oändlig excentricitet. Linjärt polariserade vågor.
Antennpolarisering
Nu när vi är medvetna om polariserade planvågselektromagnetiska fält är polariseringen av en antenn enkelt definierad.
Antennpolarisering En fjärrfältsutvärdering av antennen, polariseringen av det resulterande utstrålade fältet. Därför listas antenner ofta som "linjärt polariserade" eller "högerhänta cirkulärt polariserade antenner".
Detta enkla koncept är viktigt för antennkommunikation. För det första kommer en horisontellt polariserad antenn inte att kommunicera med en vertikalt polariserad antenn. På grund av reciprocitetsteoremet sänder och tar antennen emot på exakt samma sätt. Därför sänder och tar vertikalt polariserade antenner emot vertikalt polariserade fält. Om du försöker överföra en vertikalt polariserad horisontellt polariserad antenn kommer det därför inte att finnas någon mottagning.
I det allmänna fallet, för två linjärt polariserade antenner roterade i förhållande till varandra med en vinkel ( ), kommer effektförlusten på grund av denna polarisationsmissmatchning att beskrivas av polarisationsförlustfaktorn (PLF):
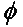
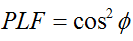
Om två antenner har samma polarisering är vinkeln mellan deras utstrålande elektronfält därför noll och det finns ingen effektförlust på grund av polarisationsfel. Om en antenn är vertikalt polariserad och den andra är horisontellt polariserad är vinkeln 90 grader och ingen effekt kommer att överföras.
OBS! Att flytta telefonen över huvudet i olika vinklar förklarar varför mottagningen ibland kan förbättras. Mobiltelefonantenner är vanligtvis linjärt polariserade, så att rotera telefonen kan ofta matcha telefonens polarisering och därmed förbättra mottagningen.
Cirkulär polarisering är en önskvärd egenskap hos många antenner. Båda antennerna är cirkulärt polariserade och lider inte av signalförlust på grund av polarisationsfel. Antenner som används i GPS-system är högercirkulärt polariserade.
Antag nu att en linjärt polariserad antenn tar emot cirkulärt polariserade vågor. Antag på motsvarande sätt att en cirkulärt polariserad antenn försöker ta emot linjärt polariserade vågor. Vad blir den resulterande polarisationsförlustfaktorn?
Kom ihåg att cirkulär polarisering egentligen är två ortogonala linjärt polariserade vågor, 90 grader ur fas. Därför kommer en linjärt polariserad (LP) antenn endast att ta emot den cirkulärt polariserade (CP) vågens faskomponent. Därför kommer LP-antennen att ha en polarisationsmissmatchningsförlust på 0,5 (-3 dB). Detta gäller oavsett vilken vinkel LP-antennen roteras. Därför:
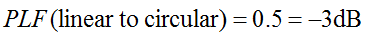
Polarisationsförlustfaktorn kallas ibland polarisationseffektivitet, antennmissmatchningsfaktor eller antennmottagningsfaktor. Alla dessa namn hänvisar till samma koncept.
Publiceringstid: 22 december 2023







