När det gällerantenner, frågan som folk är mest bekymrade över är "Hur uppnås strålning egentligen?" Hur sprider sig det elektromagnetiska fältet som genereras av signalkällan genom överföringsledningen och inuti antennen, och slutligen "separerar" det sig från antennen för att bilda en frirymdsvåg.
1. Strålning med en enda tråd
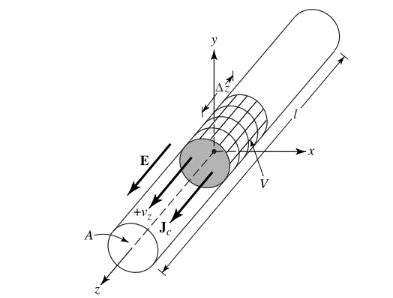
Låt oss anta att laddningstätheten, uttryckt som qv (Coulomb/m3), är jämnt fördelad i en cirkulär tråd med en tvärsnittsarea på a och en volym på V, såsom visas i figur 1.
Figur 1
Den totala laddningen Q i volym V rör sig i z-riktningen med en jämn hastighet Vz (m/s). Det kan bevisas att strömtätheten Jz på trådens tvärsnitt är:
Jz = qv vz (1)
Om tråden är tillverkad av en ideal ledare är strömtätheten Js på trådytan:
Js = qs vz (2)
Där qs är ytladdningstätheten. Om tråden är mycket tunn (helst är radien 0) kan strömmen i tråden uttryckas som:
Iz = ql vz (3)
Där ql (coulomb/meter) är laddningen per längdenhet.
Vi sysslar huvudsakligen med tunna trådar, och slutsatserna gäller för de tre ovanstående fallen. Om strömmen varierar med tiden är derivatan av formel (3) med avseende på tiden följande:
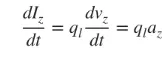
(4)
az är laddningsaccelerationen. Om trådlängden är l kan (4) skrivas enligt följande:
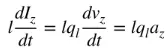
(5)
Ekvation (5) är det grundläggande förhållandet mellan ström och laddning, och även det grundläggande förhållandet för elektromagnetisk strålning. Enkelt uttryckt, för att producera strålning måste det finnas en tidsvarierande ström eller acceleration (eller retardation) av laddning. Vi nämner vanligtvis ström i tidsharmoniska tillämpningar, och laddning nämns oftast i transienta tillämpningar. För att producera laddningsacceleration (eller retardation) måste tråden böjas, vikas och vara diskontinuerlig. När laddningen oscillerar i tidsharmonisk rörelse kommer den också att producera periodisk laddningsacceleration (eller retardation) eller tidsvarierande ström. Därför:
1) Om laddningen inte rör sig, kommer det inte att finnas någon ström och ingen strålning.
2) Om laddningen rör sig med konstant hastighet:
a. Om tråden är rak och oändligt lång, finns det ingen strålning.
b. Om tråden är böjd, veckad eller diskontinuerlig, som visas i figur 2, finns det strålning.
3) Om laddningen oscillerar över tid kommer laddningen att stråla ut även om tråden är rak.
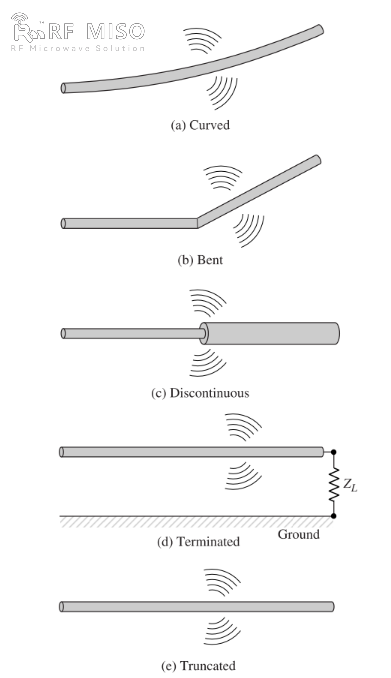
Figur 2
En kvalitativ förståelse av strålningsmekanismen kan erhållas genom att titta på en pulserad källa ansluten till en öppen tråd som kan jordas genom en last vid sin öppna ände, såsom visas i figur 2(d). När tråden initialt aktiveras sätts laddningarna (fria elektroner) i tråden i rörelse av de elektriska fältlinjer som genereras av källan. När laddningarna accelereras vid trådens källände och retarderas (negativ acceleration i förhållande till den ursprungliga rörelsen) när de reflekteras vid dess ände, genereras ett strålningsfält vid dess ändar och längs resten av tråden. Accelerationen av laddningarna åstadkoms av en extern kraftkälla som sätter laddningarna i rörelse och producerar det tillhörande strålningsfältet. Retardationen av laddningarna vid trådens ändar åstadkoms av interna krafter associerade med det inducerade fältet, vilket orsakas av ackumuleringen av koncentrerade laddningar vid trådens ändar. De interna krafterna får energi från ackumuleringen av laddning när dess hastighet minskar till noll vid trådens ändar. Därför är accelerationen av laddningarna på grund av excitationen i det elektriska fältet och retardationen av laddningarna på grund av diskontinuiteten eller den jämna kurvan hos trådimpedansen mekanismerna för generering av elektromagnetisk strålning. Även om både strömtätheten (Jc) och laddningstätheten (qv) är källtermer i Maxwells ekvationer, anses laddning vara en mer grundläggande kvantitet, särskilt för transienta fält. Även om denna förklaring av strålning huvudsakligen används för transienta tillstånd, kan den också användas för att förklara stationär strålning.
Rekommenderar flera utmärktaantennproduktertillverkad avRFMISO:
2. Tvåtrådig strålning
Anslut en spänningskälla till en tvåledarledning som är ansluten till en antenn, som visas i figur 3(a). Att applicera spänning på tvåledarledningen genererar ett elektriskt fält mellan ledarna. De elektriska fältlinjerna verkar på de fria elektronerna (lätt separerade från atomer) som är anslutna till varje ledare och tvingar dem att röra sig. Laddningarnas rörelse genererar ström, vilket i sin tur genererar ett magnetfält.
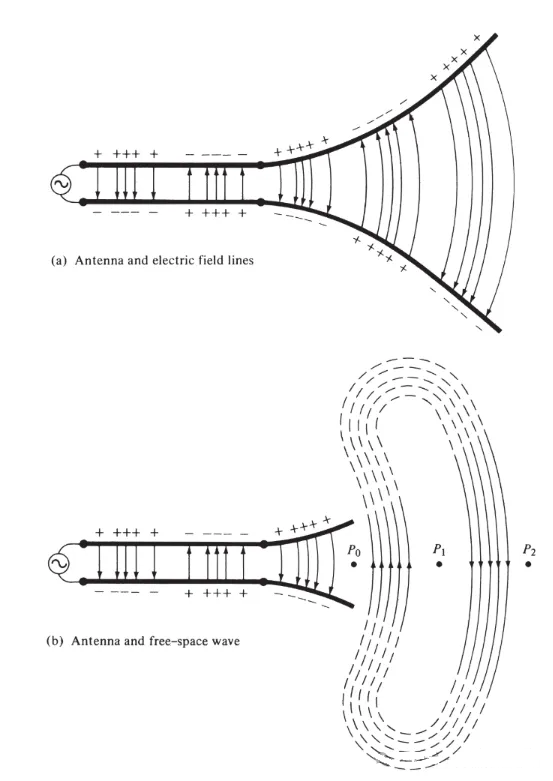
Figur 3
Vi har accepterat att elektriska fältlinjer börjar med positiva laddningar och slutar med negativa laddningar. Naturligtvis kan de också börja med positiva laddningar och sluta i oändligheten; eller börja i oändligheten och sluta med negativa laddningar; eller bilda slutna slingor som varken börjar eller slutar med några laddningar. Magnetiska fältlinjer bildar alltid slutna slingor runt strömförande ledare eftersom det inte finns några magnetiska laddningar inom fysiken. I vissa matematiska formler introduceras ekvivalenta magnetiska laddningar och magnetiska strömmar för att visa dualiteten mellan lösningar som involverar kraft och magnetiska källor.
De elektriska fältlinjerna som ritats mellan två ledare hjälper till att visa laddningsfördelningen. Om vi antar att spänningskällan är sinusformad, förväntar vi oss att det elektriska fältet mellan ledarna också är sinusformat med en period lika med källans. Den relativa magnituden av den elektriska fältstyrkan representeras av densiteten hos de elektriska fältlinjerna, och pilarna indikerar den relativa riktningen (positiv eller negativ). Genereringen av tidsvarierande elektriska och magnetiska fält mellan ledarna bildar en elektromagnetisk våg som fortplantar sig längs transmissionsledningen, som visas i figur 3(a). Den elektromagnetiska vågen kommer in i antennen med laddningen och motsvarande ström. Om vi tar bort en del av antennstrukturen, som visas i figur 3(b), kan en frirumsvåg bildas genom att "ansluta" de öppna ändarna av de elektriska fältlinjerna (visas med de streckade linjerna). Frirumsvågen är också periodisk, men konstantfaspunkten P0 rör sig utåt med ljusets hastighet och färdas en sträcka av λ/2 (till P1) på en halv tidsperiod. Nära antennen rör sig konstantfaspunkten P0 snabbare än ljusets hastighet och närmar sig ljusets hastighet vid punkter långt från antennen. Figur 4 visar fördelningen av det fria elektriska fältet för λ∕2-antennen vid t = 0, t/8, t/4 och 3T/8.
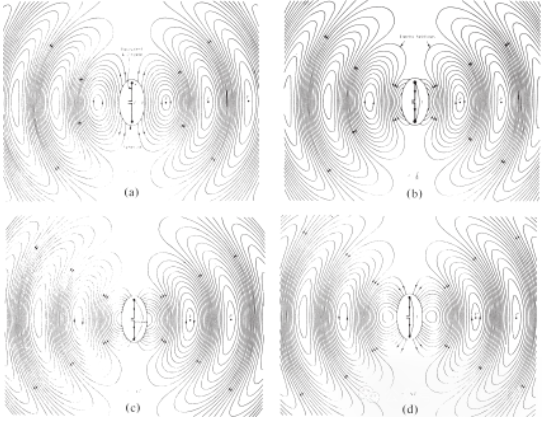
Figur 4 Fördelning av det fria elektriska fältet för λ∕2-antennen vid t = 0, t/8, t/4 och 3T/8
Det är inte känt hur de styrda vågorna separeras från antennen och så småningom formas för att fortplanta sig i det fria rymden. Vi kan jämföra styrda och fria rymdvågor med vattenvågor, vilka kan orsakas av att en sten tappas i ett lugnt vatten eller på andra sätt. När störningen i vattnet börjar genereras vattenvågor som börjar fortplanta sig utåt. Även om störningen upphör, stannar inte vågorna utan fortsätter att fortplanta sig framåt. Om störningen kvarstår genereras ständigt nya vågor, och utbredningen av dessa vågor släpar efter de andra vågorna.
Detsamma gäller för elektromagnetiska vågor som genereras av elektriska störningar. Om den initiala elektriska störningen från källan är av kort varaktighet, fortplantar sig de genererade elektromagnetiska vågorna inuti överföringsledningen, går sedan in i antennen och strålar slutligen ut som fria rymdvågor, även om excitationen inte längre finns (precis som vattenvågorna och störningen de skapade). Om den elektriska störningen är kontinuerlig existerar de elektromagnetiska vågorna kontinuerligt och följer tätt bakom dem under utbredning, vilket visas i den bikoniska antennen som visas i figur 5. När elektromagnetiska vågor finns inuti överföringsledningar och antenner är deras existens relaterad till förekomsten av elektrisk laddning inuti ledaren. Men när vågorna strålas ut bildar de en sluten slinga och det finns ingen laddning som upprätthåller deras existens. Detta leder oss till slutsatsen att:
Excitation av fältet kräver acceleration och retardation av laddningen, men bibehållande av fältet kräver inte acceleration och retardation av laddningen.
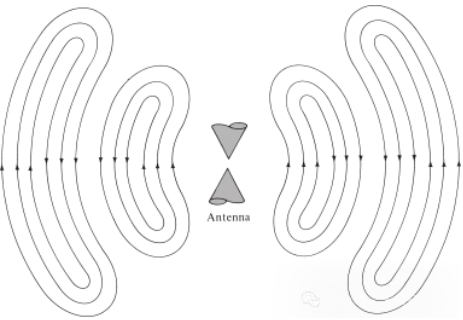
Figur 5
3. Dipolstrålning
Vi försöker förklara mekanismen genom vilken de elektriska fältlinjerna bryts loss från antennen och bildar frirumsvågor, och tar dipolantennen som exempel. Även om det är en förenklad förklaring, gör det också att människor intuitivt kan se genereringen av frirumsvågor. Figur 6(a) visar de elektriska fältlinjerna som genereras mellan dipolens två armar när de elektriska fältlinjerna rör sig utåt med λ∕4 under cykelns första kvartal. Låt oss i detta exempel anta att antalet bildade elektriska fältlinjer är 3. Under nästa kvartal av cykeln rör sig de ursprungliga tre elektriska fältlinjerna ytterligare λ∕4 (totalt λ∕2 från startpunkten), och laddningstätheten på ledaren börjar minska. Den kan anses ha bildats genom införandet av motsatta laddningar, som tar ut laddningarna på ledaren i slutet av cykelns första halva. De elektriska fältlinjerna som genereras av de motsatta laddningarna är 3 och rör sig en sträcka av λ∕4, vilket representeras av de streckade linjerna i figur 6(b).
Slutresultatet blir att det finns tre nedåtriktade elektriska fältlinjer på det första λ/4-avståndet och samma antal uppåtriktade elektriska fältlinjer på det andra λ/4-avståndet. Eftersom det inte finns någon nettoladdning på antennen måste de elektriska fältlinjerna tvingas separera från ledaren och kombineras för att bilda en sluten slinga. Detta visas i figur 6(c). I den andra halvan följs samma fysikaliska process, men observera att riktningen är motsatt. Därefter upprepas processen och fortsätter i all oändlighet, vilket bildar en elektrisk fältfördelning liknande den i figur 4.
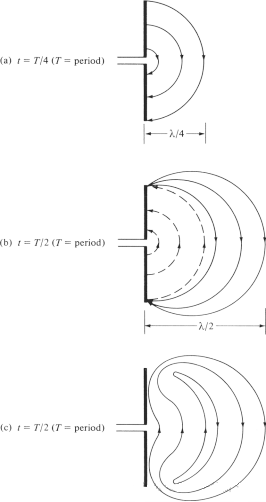
Figur 6
För att lära dig mer om antenner, besök:
Publiceringstid: 20 juni 2024










